关于机器学习，Spark MLlib中也对相关算法有API的讲解，本章介绍线性回归算法。

线性回归简介

什么是回归

  • 回归问题主要关注确定一个唯一的因变量(dependent variable)(需要预测的值)和一个或多个数值型的自变量(independent variables)(预测变量)之间的关系。
  • 广义线性回归，GLM。比如，逻辑回归，泊松回归。
  • 对于简单线性回归问题，也就是小学大家就都会了的解应用题y=a+bx。

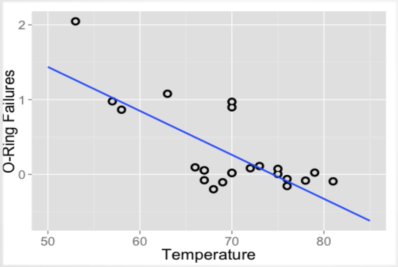
线性回归用来做预测，是一种线型有监督的预测模型。

线性回归模型保存的是权重系数 w，它是用历史数据找出规律用于预测未来。

**模型：**模型就是 y=ax1+bx2+…+d 这个公式

**建模/训练模型：**求出这个 y=ax+d

公式的过程，即用训练集数据求出 a、b 的过程。

**训练集：**参与求出 y=ax+b 公式过程的数据就是训练集，即历史数据（100万个点）

**测试集：**用于检测模型准确度的数据，应当额外寻找一些数据来测试，将训练集的数据排除在外。

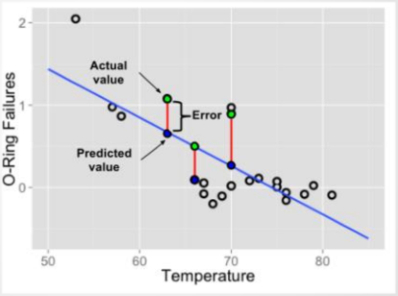
损失函数（误差函数）：

J(θ0,θ1)=12m∑i=1m(hθ(xi)−yi)2J(\theta_0,\theta_1)=\frac{1}{2m}\sum_{i=1} ^m(h_\theta(x^i) - y^i)^2

**拟合函数：**y = ax + b

最小二乘法

一个点 (x1,y1) 误差：(ax1 + b - y1) ²

多个点的误差，又叫损失函数：

二维：

三维：

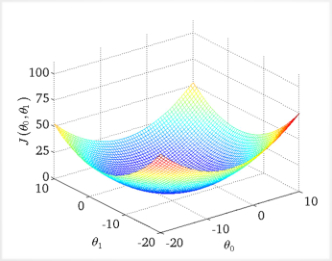
梯度下降法

用于快速找到误差最小值。

梯度下降法就是一个寻找一座山最低谷的过程。
1、如果当前往前走是上山，那么就后退；
2、如果当前往前走是下山，那么就前进；
3、不停的走，每走一步看下当前路况，决定下一步是前进还是后退，如此反复。

基本步骤：

  • 先确定向下一步的步伐大小，我们称为Learning rate；
  • 任意给定一个初始值；
  • 确定一个向下的方向，并向下走预先规定的步伐，并更新；
  • 当下降的高度小于某个定义的值，则停止下降。

问题

  • 如果初始值就在local minimum的位置，则会如何变化？
  • 如果取到一个正确的值，则cost function应该越来越小，怎么取值@
  • @过大会有什么问题？
  • 过拟合怎么解决？

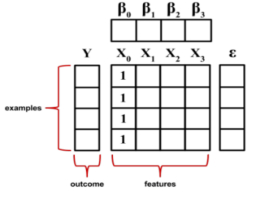
多元线性回归

大多数现实世界的分析不止一个自变量，大多数情况下，很有可能使用多元线性回归。

相关系数

两个变量之间的相关系数是一个数，它表示两个变量服从一条直线的关系有多么紧密。

关系数就是指Pearson相关系数，它是数学家Pearson提出来的，相关系数的范围是[-1,1]之间，两端的值表示一个完美的线性关系。