SparkMLlib Kmeans聚类
Kmeans聚类算法又叫K均值聚类。
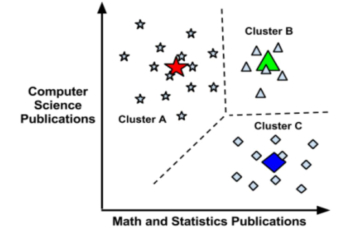
聚类:给事物打标签,寻找同一组内的个体之间的一些潜在的相似模式。力图找到数据的自然分组 kmeans。
理解Kmeans聚类算法
聚类是一种无监督的机器学习任务,它可以自动将数据划分成类 cluster。因此聚类分组不需要提前被告知所划分的组应该是什么样的。因为我们甚至可能都不知道我们再寻找什么,所以聚类是用于知识发现而不是预测。
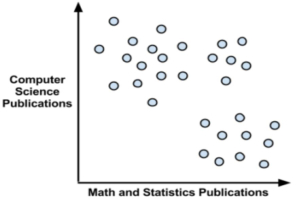
聚类原则是一个组内的记录彼此必须非常相似,而与该组之外的记录截然不同。所有聚类做的就是遍历所有数据然后找到这些相似性。
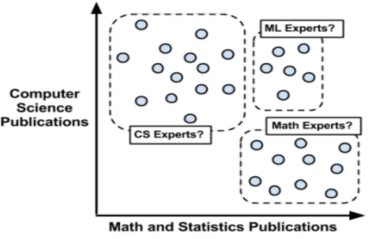
- 使用距离来分配和更新类
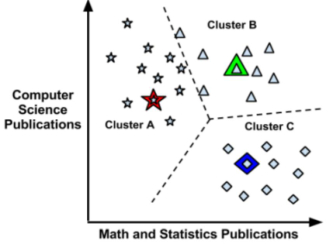

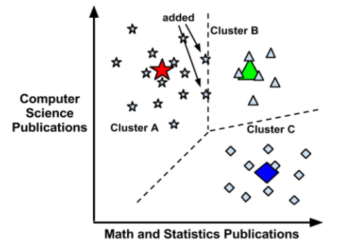
探究距离测度
-
欧氏距离测度(EuclideanDistanceMeasure)
-
平方欧氏距离测度(SquaredEuclideanDistanceMeasure)
-
曼哈顿距离测度(ManhattanDistanceMeasure)
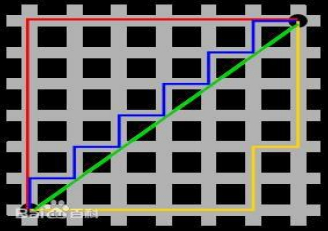
图中红线代表曼哈顿距离,绿色代表欧氏距离,也就是直线距离,而蓝色和黄色代表等价的曼哈顿距离。曼哈顿距离——两点在南北方向上的距离加上在东西方向上的距离,即d(i,j)=|xi-xj|+|yi-yj|。对于一个具有正南正北、正东正西方向规则布局的城镇街道,从一点到达另一点的距离正是在南北方向上旅行的距离加上在东西方向上旅行的距离,因此,曼哈顿距离又称为出租车距离。
- 余弦距离测度(CosineDistanceMeasure)
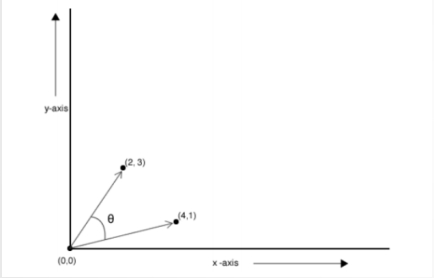
-
谷本距离测度(TanimotoDistanceMeasure)
同时表现夹角和距离的距离测度。
-
加权距离测度(WeightedDistanceMeasure)
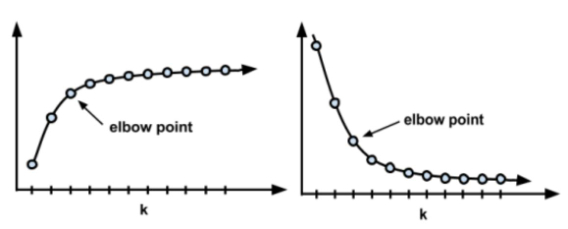
选择适当的聚类数
- 肘部法
Kmeans算法
以空间中K个点为中心进行聚类,对最靠近他们的对象归类,通过迭代的方法,逐次更新各聚类中心的值,直到得到最好的聚类结果。
聚类的结果跟开始的选点有关。
Kmeans 流程
1、适当选择c个类的初始中心。
2、在第K次迭代中,对任意一个样本,求其到c各中心的距离,将该样本归到距离最短的中心所在的类。
3、利用均值等方法更新该类的中心值。
4、对于多有的c个聚类中心,如果利用2,3的迭代法更新后,值保持不变,则迭代结束,否则继续迭代。
Kmeans动图演示:
上选点:
下选点:
左选点:
右选点:
Kmeans 算法缺陷
-
聚类中心的个数K 需要事先给定,但在实际中这个 K 值的选定是非常难以估计的,很多时候,事先并不知道给定的数据集应该分成多少个类别才最合适。
-
Kmeans需要人为地确定初始聚类中心,不同的初始聚类中心可能导致完全不同的聚类结果。(可以使用Kmeans++算法来解决)。
Kmeans++算法
Kmeans++在开始的选点上进行了优化,减少了人为选点的影响,同时类与类之间的差异也比较大。
Kmeans++ 流程
1、从输入的数据点集合中随机选择一个点作为第一个聚类中心;
2、对于数据集中的每一个点x,计算它与最近聚类中心(指已选择的聚类中心)的距离D(x);
3、选择一个新的数据点作为新的聚类中心,选择的原则是:D(x)较大的点,被选取作为聚类中心的概率较大;
4、重复2和3直到k个聚类中心被选出来;
5、利用这k个初始的聚类中心来运行标准的k-means算法。
Kmeans++演示动图:

聚类的原则
1、类的成员之间越相似越好。
2、类之间的成员差异越大越好。






