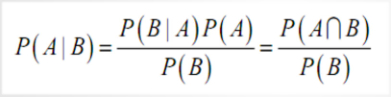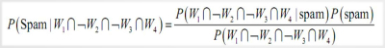SparkMLlib贝叶斯分类

机器学习算法中，有种依据概率原则进行分类的朴素贝叶斯算法，正如气象学家预测天气一样，朴素贝叶斯算法就是应用先前事件的有关数据来估计未来事件发生的概率。如：70%降水概率。

贝叶斯分类算法是一个非线性有监督的分类算法。

贝叶斯分类用于做概率分类。二分类、正负例。

贝叶斯条件概率

思考：

一所学校里面有 60% 的男生，40% 的女生。男生总是穿长裤，女生则一半穿长裤一半穿裙子。假设你走在校园中，迎面走来一个穿长裤的学生（很不幸的是你高度近视，你只看得见他（她）穿的是否长裤，而无法确定他（她）的性别），你能够推断出他（她）是男生的概率是多大吗？

基于贝叶斯定理的条件概率

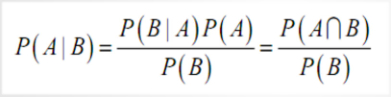
通过此公式可以算出上题：

理解朴素贝叶斯

如果我们知道P（垃圾邮件）和P（Viagra）是相互独立的，则容易计算P（垃圾邮件&Viagra），即这两个事件同时发生的概率。 20% * 5% = 1%​

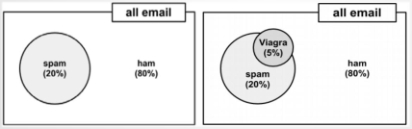
对于我们垃圾邮件来说

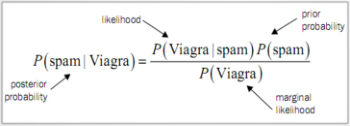
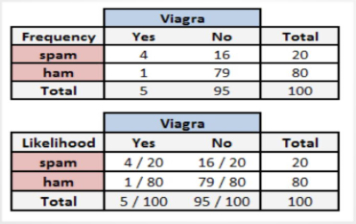
计算贝叶斯定理中每一个组成部分的概率，我们必须构造一个频率表

$P(垃圾邮件|Viagra) = P(Viagra|垃圾邮件) * P(垃圾邮件) / P(Viagra)$

$= (4/20) * (20/100) / (5/100) = 0.8$

因此，如果电子邮件含有单词Viagra，那么该电子邮件是垃圾邮件的概率为80%。所以，任何含有单词Viagra的消息都需要被过滤掉。

当有额外更多的特征是，这一概念如何被使用

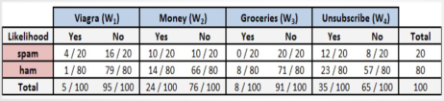
利用贝叶斯公式，我们得到概率如下：

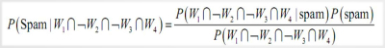
• 分母可以先忽略它，垃圾邮件的总似然为：

  $(4/20) * (10/20) * (20/20) * (12/20) * (20/100) = 0.012$

• 非垃圾邮件的总似然为：

  $(1/80) * (66/80) * (71/80) * (23/80) * (80/100) = 0.002$

• 将这些值转换成概率，我们只需要一步得到垃圾邮件概率为85.7%

问题

现在有一封邮件，它包含了这四个单词，那么这封邮件是垃圾邮件的概率多大呢

• 可以计算垃圾邮件的似然如下：

  $(4/20) * (10/20) * (0/20) * (12/20) * (20/100) = 0$

• 非垃圾邮件的似然为：

  $(1/80) * (14/80) * (8/80) * (23/80) * (80/100) = 0.00005$

• 该消息是垃圾邮件的概率为

  $0 / (0+0.00005) = 0$

• 该消息是非垃圾邮件的概率

  $0.00005/(0+0.00005)=1$

问题出在Groceries这个单词，单词Grogeries有效抵消或否决了所有其他的证据。

拉普拉斯估计

拉普拉斯估计解决了每个特征的概率非零。

拉普拉斯估计本质上是给频率表中的每个计数加上一个较小的数，这样就保证了每一类中每个特征发生概率非零。

通常情况下，拉普拉斯估计中加上的数值设定为1，这样就保证每一个特征至少在数据中出现一次。

• 然后，我们得到垃圾邮件的似然为：

  $(5/24) * (11/24) * (1/24) * (13/24) * (20/100) = 0.0004$

• 非垃圾邮件的似然为：

  $(2/84) * (15/84) * (9/84) * (24/84) * (80/100) = 0.0001$

• 这表明该消息是垃圾邮件的概率为80%，是非垃圾邮件的概率为20%。

实例：

利用普氏贝叶斯对邮件进行分类（正常邮件和垃圾邮件）

1、构建词袋：采用稀疏向量

2、文本向量化

3、输入文本