SparkMLlib 逻辑回归
逻辑回归是预测分类响应的常用方法。这是广义线性模型的一个特例,可以预测结果的概率。
在spark.ml逻辑回归中,可以使用二项逻辑回归来预测二元结果,或者可以使用多项逻辑回归来预测多类结果。使用该family 参数在这两种算法之间进行选择,或者保持不设置,Spark将推断出正确的变量。
逻辑回归的基本概念
逻辑斯蒂回归(logistic regression)是统计学习中的经典分类方法,属于对数线性模型。logistic回归的因变量可以是二分类的,也可以是多分类的。
逻辑回归与线性回归的区别:
线性回归中 y 的值域在[-∞,+∞],不能很好的表示;
逻辑回归通过 sigmod 函数将线性回归作为一个系数传进来,值域被映射为[0,1],然后比如大于0.5为一类,小于0.5为一类
补充:
1、逻辑回归本质是求解二分类问题,一般所谓的预测就是分类;
2、所有的多分类的问题都可以转化为多个二分类的问题;
3、在Spark MLlib中二分类的话,1为正例,0为负例。
归结一句话就是:逻辑回归是一种线性有监督分类模型。
逻辑回归的公式:
其中的 z=w_1x_1+w_2x_2+w_3x_3+…+w_nx_n+w_0,相当于多元线性回归。
使用案例
-
在医学界,广泛应用于流行病学中,比如探索某个疾病的危险因素,根据危险因素预测疾病是否发生,与发生的概率。比如探讨胃癌,可以选择两组人群,一组是胃癌患者,一组是非胃癌患者。因变量是“是否胃癌”,这里“是”与“否”就是要研究的两个分类类别。自变量是两组人群的年龄,性别,饮食习惯,等等许多(可以根据经验假设),自变量可以是连续的,也可以是分类的。
-
在金融界,较为常见的是使用逻辑回归去预测贷款是否会违约,或放贷之前去估计贷款者未来是否会违约或违约的概率。
-
在消费行业中,也可以被用于预测某个消费者是否会购买某个商品,是否会购买会员卡,从而针对性得对购买概率大的用户发放广告,或代金券等等,进行精准营销。
前面我们说到过逻辑回归是一种用于分类的模型,就相当于y=f(x),表明输入与输出(类别)的关系。最常见问题有如医生治病时的望、闻、问、切,之后判定病人是否生病或生了什么病,其中的望闻问切就是输入,即特征数据,判断是否生病就相当于获取因变量y,即分类结果。
案例:逻辑回归应用于二分类问题
个人信用预测
保险公司在卖保险时,根据个人基本信息判断获赔概率
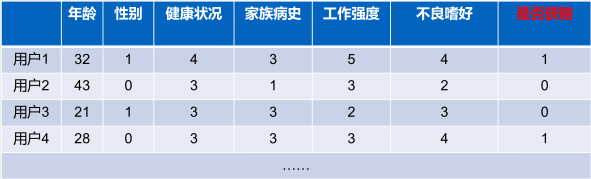
二分类:
要么A类,要么B类
比如人的身体状况为2中:1.健康;2生病
健康的可能性是1,生病的可能性就是0;
健康的可能性是0.8,生病的可能性是0.2;
健康的可能性是0.3,生病的可能性是0.7。
逻辑回归二分类:测试结果>0.5为正例----获赔,测试结果y<0.5为负例—不获赔
训练集:健康状况训练集
在案例问题中:
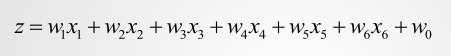
训练:
确定w的过程,就是训练过程,spark的mllib已经做好了封装,只需调用即可
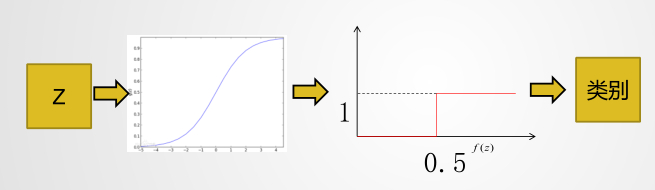
**singmod函数:**singmod函数为将线性变为非线性
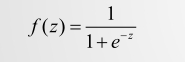
函数图
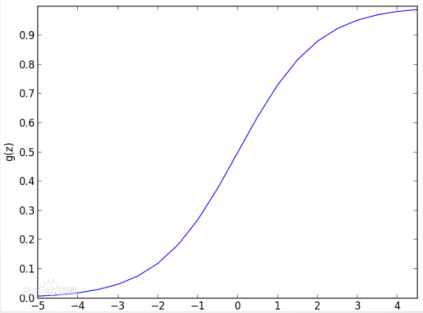
如何判定结果:
Spark MLlib中应用逻辑回归解决二分类问题的代码:
import org.apache.spark.mllib.classification.{LogisticRegressionWithLBFGS} |
那么,上面的代码是中所谓的训练模型到底是怎么回事呢?
请看图:

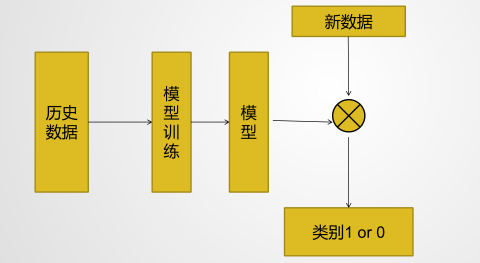
何为训练模型:
从历史数据中,我们可以知道,个人的健康状况和用户的特征息息相关(),因此通过 和初始 (初始值一般不全为0),通过逻辑回归将 带入 中,从而得到一个预测的健康状况。然后将真实的健康状况和预测的健康状况进行对比求错误,然后通过错误,不断的调整 的值,反复迭代。直到错误接近于 0 的最优解,即错误最小的时刻。那么对应的模型 即为最后的模型。
如何最快的求错误最小的时刻?-----调优,后面详细讲解
有了训练出来的模型后就要测试模型的准确度,将测试数据带入模型即可求解:
换一种角度理解逻辑回归:逻辑回归分界线
既然逻辑回归是线性有监督的分类模型,那么对于分类,分类的分界线在哪里呢?
对于二分类来说那肯定是0.5:
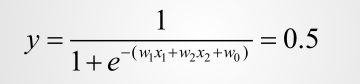
很明显,求解分界线就是求解方程组:
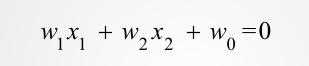
那么就有:
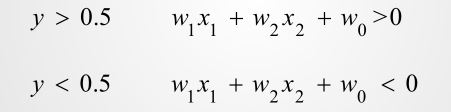
那么 ,对应于平面的一条直线,这条分解线就是分类线,将类别划分开来:
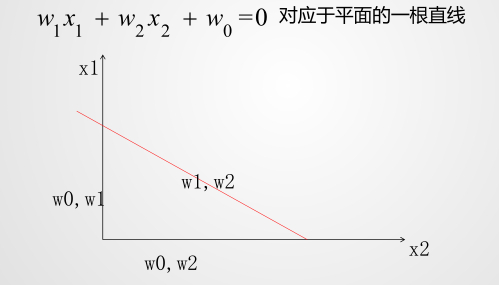
对应当其类比到高维空间,也是同样的原理。
三维的需要一个平面作为分界线,四维的需要立体空间作为分界线 . . .
总结一句就是:
**求模型就是根据已知的数据集寻找分界线,平面,立体空间 . . . **
对于二分类即找到一条直线将数据切分开,那么有无,对构成什么样的直线就很重要了

我们知道直线的公式是:,有无 ,即如图:
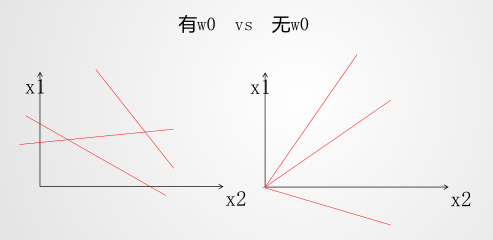
那么总结一句:逻辑回归的本质:就是有w0 vs 无w0
现在我们用代码来测试一下:
import org.apache.spark.mllib.classification.{LogisticRegressionWithLBFGS, LogisticRegressionWithSGD} |
是否应该有w0的测试数据:
测试过后你会明显的发现,有无正确率差异比较大。
逻辑回归遇到线性不可分
刚刚还说逻辑回归是线性有监督的分类模型,既然是线性的,那么就会遇到线性不可分的问题:
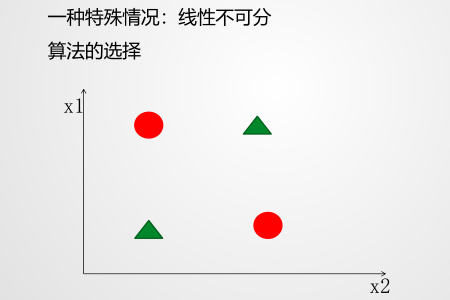
上面图中,你找不到一条线可以将其数据分开的,这个就是线性不可分问题,那么怎么解决呢?
升维解决线性不可分的问题:
一般是将已知的维度两两相乘,将其映射到高维的空间,那么就能找到一个平面将其分开。
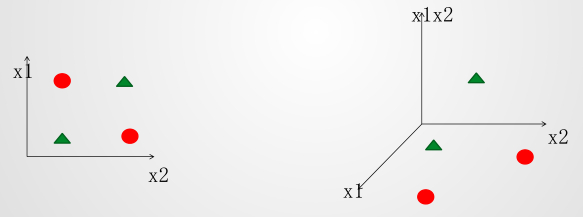
Spark Mllib中代码演示
import org.apache.spark.mllib.classification.{LogisticRegressionWithLBFGS, LogisticRegressionWithSGD} |
线性不可分数据集:
测试过后你会明显的发现,升维过后正确率有明显的上升。
在真实的生产中,轻易间一般不会出现线性不可分的升维问题,只有当出现准确率大幅度下降的时候猜测应该是线性不可分的问题时候,才特征两两组合升维,测试看效果。
总结:
逻辑回归是一种线性 有监督分类模型,既然是有监督的,那么数据集中就应该有要预测的真实数据 y,既然是分类问题,那么有无 就很影响正确率,既然是线性模型,那么就会遇到线性不可分的问题,轻易间一般不会出现线性不可分的升维问题,当出现准确率大幅度下降的时候猜测应该是线性不可分的问题时候,才特征两两组合升维,测试看效果。
关于阈值分析
逻辑回归是求解二分类问题,那么分类的阈值是:结果>0.5为正例,结果<0.5为负例
首先,先来思考一个问题?判断一个病人是否患癌症,判断情况(1)的风险大,还是判断情况(2)的风险大?
(1): 假如病人是癌症:
– 判断成不是癌症<0.5
(2)假如病人是非癌症:
– 判断是癌症>0.5
当然,很多人认为是第二种情况是糟糕的,但是第一种情况的后果更加的严重,病人承受的风险会加大,那么我们怎么通过调优模型来规避这样的风险呢?
我们可以不使用逻辑回归的默认的分类阈值0.5,去除固定的阈值0.5,根据业务场景调整相应的情况调整阈值,比如说0.3, 虽然整体的错误率变大了,但是规避了一些不能接受的风险。
很明显,当你规避了一些不能接受的的风险以后,相应的模型的正确率下降了,错误率提高了。
好,现在使用之前的健康状况数据集,使用Spark MLlib的封装函数测试:
import org.apache.spark.mllib.classification.{LogisticRegressionWithLBFGS, LogisticRegressionWithSGD} |
误差的优化:梯度下降分析
前面提到了训练模型的过程,现在再来思考一下:
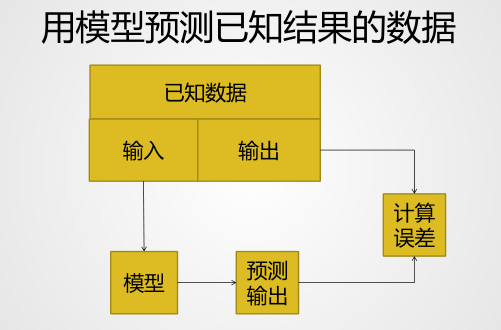
图中的计算误差是一个反复迭代的过程,相应的调整模型W,那么怎么样才能求得最小的误差,获得最好的模型呢?其中我们可以使用一种叫梯度下降的方法(GD–gradient descent)
先看逻辑回归的误差函数:
这个是其中的一个数据的误差函数:
参数解释:
T为线性代数中的矩阵转置

那么,逻辑回归的 singmod 函数就变成了:
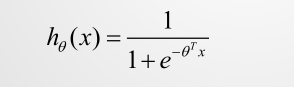
我们将类比下图看误差函数:
对于一组参数:
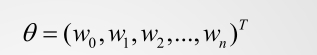
对应误差:
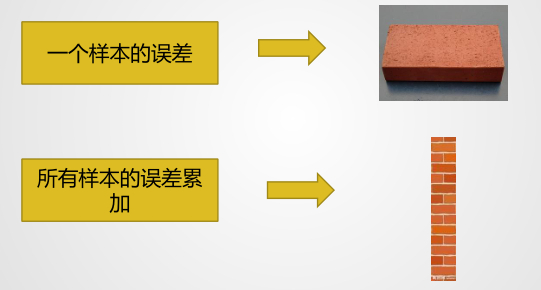
那么对于所有的参数,总误差就是:

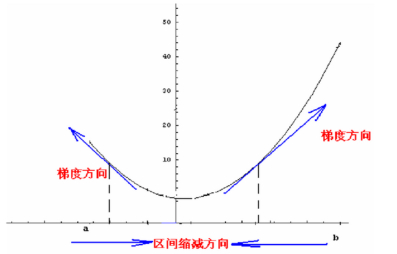
很明显,找到参数对应的最矮的那堵墙的时候,就找到了最小的误差,上图最小的误差是参数4对应的误差,那么怎么才能以最快的速度求解最小的误差呢?在无数的参数对应的误差有点类似于一座山,现在考虑的就是怎么以最快的速度下山的问题?

怎么以最快的速度下山呢?-----随机梯度下降法
最快的下山的方式是每次都走 “最陡峭的道路”,最陡峭的道路很明显是最 “斜率” 的绝对值最大的,当走完上次最陡峭的路后,然后再找到最陡峭的路,直到走到谷底,这个过程就是随机梯度下降法。
SGD(随机梯度下降法)就是一种优化误差函数的方法:以最快的速度求解最小误差。
所谓的梯度就是斜率,每次都找到斜率的绝对值最大的,然后就能最快的求解最小的误差。
说白了就是求误差函数斜率为 0 的时刻!!!
那么训练的目的就是找到合适的 θ ,使得整体误差最小,即达到山底。
即最小化下式:
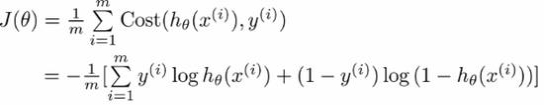
上面的误差函数被证明是凹函数(有极小值,无极大值),存在全局最优解,那么求解最小值的过程就是求解极值的过程。求极值就是让导数等于0,求解 θ ,也就是 w_0,w_1,w_2,…,w_n
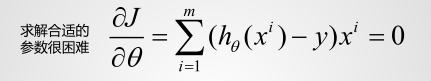
但是从上函数可以看到几乎无法求解!
对于误差函数求导是比较困难,我们可以逆向思维,带入不同的 ,反复的迭代直到找到斜率为0的时刻。
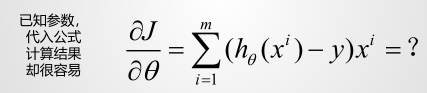
那么就有:


误差 J 随 θ变化图:
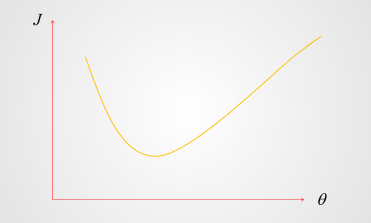
把误差函数当成一座山,梯度就是往前走时陡峭程度的数字化表现。
- 绝对值越大,此时山越陡峭
- 梯度>0,往前走是上山
- 梯度<0,往前走是下山
- 梯度=0,山谷或者山峰
总结:
梯度下降法就是一个找寻一座山最低谷的过程:
- 如果当前往前走是上山,那么就后退;
- 如果当前往前走是下山,那么就前进;
- 不停的走,每走一步看下当前路况,决定下一步是前进还是后退,如此反复。
公式表示为:
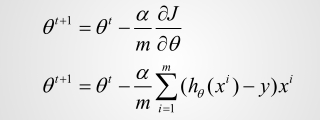
梯度下降示意图:
鲁棒性调优
鲁棒性出现的原因和目的:
原始误差过于拟合,牺牲一些正确率来提高推广能力,防止过拟合!!!
鲁棒性调优的作用:
让你的模型更加的健壮,提高模型的通用性,推广能力、泛化能力。
对于表达式:w_1x_1+w_2x_2+w_0=0,对应于平面一条直线
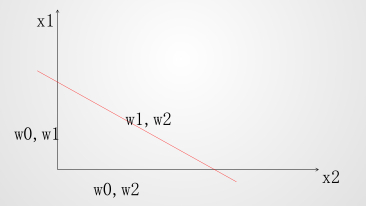
下述两个公式描述同一条直线,哪个好?

在求 z 的过程中:z=w_1x_1+w_2x_2+w_3x_3+…+w_nx_n,如果 w 越大,求得的 z 对逻辑回归的 sigmoid 函数影响就越大,抗干扰的能力就越小,小小的变化就会影响到最后的分类结果。
总结:W 越小,模型的抗干扰能力越强。
肯定,不是说 w 越小就越好,那怎么找到一组适合的最小W呢?
加上正则提高你模型的推广能力-----设置lambda系数
首先来看正则化公式:
L1正则>0: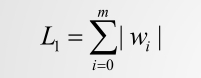
L2正则>0: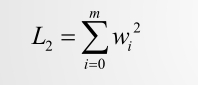
为了提高模型的泛化能力(推广能力—不过拟合----适应更多的未来的新的数据,做到举一反三),需要重写误差函数,加入认为的惩罚系数 :

lambda( λ )是系数,区间在[0,1]:
lambda是 w 的权重,因此我们可以通过调整 lambda 的大小来决定是更加的看重模型的准确率还是更加的看重模型的推广能力,一般情况从经验来看,会把 lambda 设置为0.4
重写误差函数必定会牺牲一定的正确率,但是能提高模型的推广能力。牺牲正确率来提高推广能力!!!
正则 L1 和L2 怎么选择呢 – 区别?
L1更加的倾向于使得 要么取1,要么取0。也称为(lasso回归)稀疏编码,可用来降维。
L2更加的倾向于使得 整体偏小。也称为岭回归(rige回归)
一般L2更常用
关于回归技术,请参考:http://www.csdn.net/article/2015-08-19/2825492
Spark MLlib中的实现L1或者L2代码测试:
import org.apache.spark.mllib.classification.{LogisticRegressionWithLBFGS, LogisticRegressionWithSGD} |
训练方法优化
在 Spark MLlib 中 SGD 和 LBFGS 实现的区别:

拟牛顿法(LBFGS):val lr = new LogisticRegressionWithLBFGS,求二阶导数,相比SGD能更快更准确的收敛,每次迭代用到的训练集里面全部的数据,还可以做多分类。没有L1正则化,只有L2正则化(当不需要L1正则化时,强烈建议使用LBFGS)
随机梯度下降算法(SGD):val lr = new LogisticRegressWithSDG,求一阶导数,相比基础梯度下降算法,它无需环顾四周360°,每次迭代随机抽取一部分训练集数据,求导,只能做二分类。L1和L2正则化都有。
L- BFGS 为 SGD 的优化方法,它的训练速度比 SGD 快。
数值优化
数值优化不会影响正确率,只会提升求解模型的速度!
数值优化一
案例:某个地区的生态环境和动物数量的关系
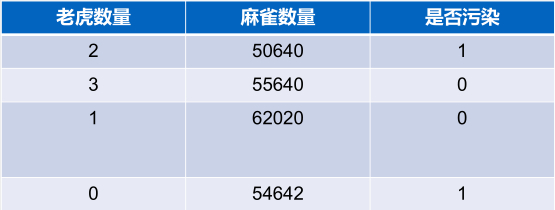
观察上面的老虎的数量和麻雀的数量,可以知道老虎的数量和麻雀的数量差别很大,那么这样的输入数据会造成什么样的后果呢?
论点A:各个维度的输入如果在数值上差异很大,那么会引起正确的 w 在各个维度上数值差异很大。
论点B:找寻 w 的时候,对各个维度的调整基本上是按照同一个数量级来进行调整的(随机梯度下降的步长是一样的)。
发现 A 和 B 两条结论互相矛盾!!!
因为:0=w_1x_1+w_2x_2+w_3x_3+…+w_nx_n,当 x 的值差异很大的时候, 的值也差异很大。
解决X的值差异很大的解决方案?------归一化
归一化的方法:
(1)最大值最小值法 min-max标准化(Min-Max Normalization)
公式: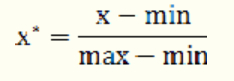
**优点:**归一化的值一定在0~1之间
**缺点:**缺点是抗干扰能力弱,受离群值得影响比较大,导致0~1之间分布不均匀,中间容易 没有数据。
(2)方差归一化
**优点:**抗干扰能力强,和所有数据都有关,求标准差需要所有值的介入,重要有离群值的话,会被抑制下来。
**缺点:**是最终未必会落到0到1之间,牺牲归一化结果为代价提高稳定。
优化后:



总结:
归一化的目的:归一化的目的是消除 x 之间的过大差异,从而消除 w 之间的过大差异,从而使得在训练(梯度下降法)的时候,使得 w 之间的变化是同步、均匀的,从而使得你求解机器学习模型的速度加快!
数值优化二
在训练模型,不断的调整 w 的时候:

参数解释:
x_{i1}和 x_{i2} 是历史数据
α 是调整的步长
A 是斜率
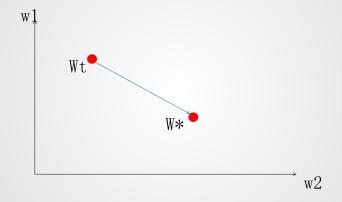
是 t 时刻的 ,是 t+1 时刻的 ,在不断的调整 的时候,是随着 同时变化的
问题: 和 只能朝一个方向变化。要么同时变大,要么同时变小

如上图:以最快的速度从 到 时刻,直线是最快的,调整 W 的时候,沿着蓝线的方向调整, 减小, 变大。
从上面的公式,我们知道数据 决定了 的调整方向,让 有正有负就能调整 的方向。
因此,解决方法:尽可能让 x 的各个维度取值上有正有负!
均值归一化—每个数量减去平均值
方差归一化,均值归一化后:
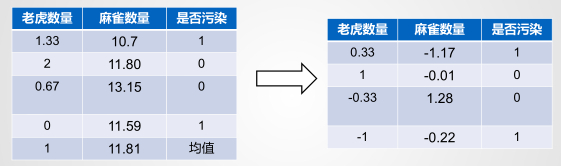
均值归一化后,沿着正确的方法调整 的可能性更大,求解 的速度更快了
测试数据集:
Spark MLlib实现数值优化代码:
import org.apache.spark.mllib.classification.{LogisticRegressionWithLBFGS, LogisticRegressionWithSGD} |
逻辑回归总结
Logistic Regression:是一种线性有监督的分类模型。
1、设置
因为如果不设置 就会使得分界一定会穿过原点,这样就会使得计算的模型受到很大的局限性,设置方法:lr.setIntercept(true)
2、线性不可分
遇到线性不可分的问题,需要升高维度,方法是让已有的维度俩俩相乘来构建更多的维度。
.map { labelpoint => |
3、Threshold 阈值
Threshold 阈值在 LR 里面默认是根据 0.5 来进行二分类的,为了去规避一些风险,我们可以去掉阈值,这样最后 LR 给的结果就是0到1之间的一个分值,我们可以根据分值,自己来定到底属于哪个类别
TradeOff:人为的去调整阈值,最后的正确率一定会下降
val model = lr.run(trainingData).clearThreshold() |
4、鲁棒性调优
鲁棒性:模型的通用性,举一反三的能力,推广能力,泛化能力
尽可能在保证正确率的情况下,使得W越小越好!
好到什么程度?
定义 L1 正则化和 L2 正则化,然后重写误差函数让算法去减小误差的同时减小 L1 或 L2。
L1:有的趋近于1,有的趋近于0,稀疏编码
L2:整体的W同时变小,岭回归
TradeOff: 人为的去重写了误差函数,会导致最后的正确率一定会下降
lr.optimizer.setUpdater(new SquaredL2Updater) |
5、数值优化
(1)方差归一化:会考虑到一组数里面的所有数据,就是每个数去除以方差
优点:就是会使得各个W基本数量级一致
缺点:所有的值未必都会落到0到1之间
(2)均值归一化:让找到最优的速度变快,让各个维度的数据有正有负,就会使得各个W在调整的时候有的变大有的变小
val scalerModel = new StandardScaler(withMean=true, withStd=true).fit(vectors) |
6、SGD 和 LBFGS的区别
SGD:随机梯度下降法,每次迭代随机抽取一部分训练集数据,求导,只能做二分类。
LBFGS:拟牛顿法,速度比较快求二阶导数,每次迭代用到训练集里面所有的数据,还可能做多分类。
公司使用:直接使用 LBFGS
val lr=new LogisticRegressionWithSGD() |






